Panel Data Regression in R
Alex Marsella
2022-08-14
This tutorial covers the structure of panel data and how fixed effects help us improve our measure of “the effect”. It is made with the students of my Applied Economic Research class in mind.
Topics touched on in this tutorial include:
- Loading built-in datasets for practice.
- The power of
ggplotfor helping us think about our data. - Working with panel data.
- Understanding why fixed effects are so commonplace in modern statistical analysis.
- Understanding what fixed effects do to our analysis.
- Closing some backdoors in a directed acyclical graph (DAG).
- Fixed effects regressions with base R’s
lmandfelmfrom the packagelfe. - Clustering standard errors and why we do it.
Certain datasets qualify as “panel data” because they are made of repeated cross-sections of unit-level observations over time. In other words, a time-series of cross-sections. For this tutorial, we will load a basic panel data set called “Grunfeld”, which is built into the package plm. When a dataset is built into R in this way, it can be loaded without a call to a file in your computer.
The data Grunfeld is a panel data set of 10 firms over 20 years. For every firm-year observation, it contains gross investment, value of the firm, and capital stock for the firm. As always, we load tidyverse because it contains packages such as dyplr, ggplot2, and more.
library(tidyverse)
library(plm)
data("Grunfeld", package = "plm")
head(Grunfeld)## firm year inv value capital
## 1 1 1935 317.6 3078.5 2.8
## 2 1 1936 391.8 4661.7 52.6
## 3 1 1937 410.6 5387.1 156.9
## 4 1 1938 257.7 2792.2 209.2
## 5 1 1939 330.8 4313.2 203.4
## 6 1 1940 461.2 4643.9 207.2ggplot is included in tidyverse. It is not as straightforward as base R plotting, but it is much more powerful. Let’s examine the relationship between capital stock and gross investment for firms.
ggplot(Grunfeld, aes(x=capital, y=inv)) + #tells ggplot to look at Grunfeld and which variables to use
geom_point() + xlab("Stock of plant and equipment") + ylab("Gross Investment")+ #without geom_point(), our plot is blank
geom_smooth(method="lm", se =FALSE) #regresses y on x and adds a line to the plotAt first glance, we can see that the firm-years with very high levels of capital certainly have high levels of investment. However, this does not tell us very much. We have not considered the fact that there are many firms and years. Note how poor of a fit a single regression line gives us over this scatter plot. This regression line is equivalent to running the following code:
reg1 <- lm(inv~capital, data=Grunfeld)
summary(reg1)##
## Call:
## lm(formula = inv ~ capital, data = Grunfeld)
##
## Residuals:
## Min 1Q Median 3Q Max
## -316.92 -96.45 -14.43 17.07 481.92
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 14.23620 15.63927 0.91 0.364
## capital 0.47722 0.03834 12.45 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 162.9 on 198 degrees of freedom
## Multiple R-squared: 0.439, Adjusted R-squared: 0.4362
## F-statistic: 154.9 on 1 and 198 DF, p-value: < 2.2e-16It seems that the expected investment is 14.24 when capital stock is 0,1 and each unit (presumably one dollar) of capital stock is correlated with 0.48 units (presumably 48 cents) more investment. Is this really useful, though? We have not considered that a one-size-fits-all intercept provides a very poor fit to many of the points on the plot. Let’s try coloring our plot by firm ID and thinking about firm-specific effects. This is where ggplot really shines.
ggplot(Grunfeld, aes(x=capital, y=inv, colour=factor(firm))) + #we have to declare the color scheme here
geom_point() + xlab("Stock of plant and equipment") + ylab("Gross Investment") +
scale_colour_discrete(name="Firm") + #without this, our key will say "factor(firm)", which looks bad
geom_smooth(method="lm", se =FALSE)Now that the points are colored by firm ID, it becomes clearer that one firm is systemically larger than all of the others. Consider how, when “stock of plant and equipment” is under 250, most firms’ “gross investment” looks to be around 100. For firm 1, though, the gross investment value is above 500. It’s possible that the relationship (the slope) is similar among all of the firms, but the intercept clearly varies. In other words, the starting value for “gross investment” (when stock=0) is much higher for firms 1 and 2. If we add firm fixed effects to our regression model, the model will account for a time-invariant intercept for each firm.
That being said, we have not even considered the problem of time just yet. The same way some firms are systemically different than others, with different CEOs, locations, etc., there could be universal characteristics that change from year to year. This data spans the tail-end of the great depression, extends through world war 2, and finishes during the post-war economic boom. Year fixed effects can capture all of that effect if we assume all firms are affected equally!2
Let’s think about the DAG. By using a package called DiagrammeR, the mermaid command allows us to make our own DAG.
library(DiagrammeR)
mermaid("
graph LR
C(Stock of plant and equipment)-->I(Gross Investment)
T(Time-varying unobservables affecting all firms equally)-->I
T-->C
F(Time-invariant unobservables specific to each firm)-->C
F-->I
") #note that each variable only needs to be defined once, after which you can use a single letter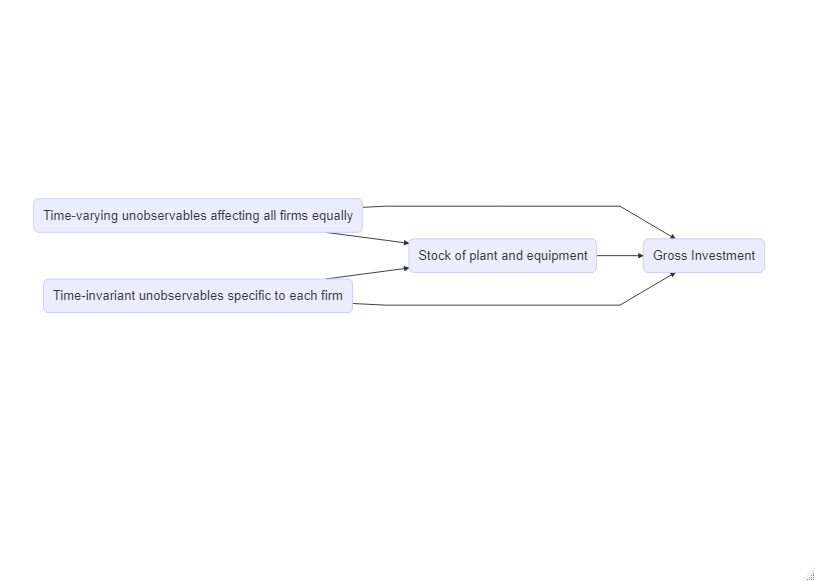
This DAG offers an overly verbose hint as to why “two-way fixed effects” is so common in regressions using panel data. Over time, there are factors that affect all firms’ capital stock and gross investment, such as macro-economic growth and technological progress. In addition, some firms may simply be “large” and others “small”, some firms may have better management,etc. This would clearly have an effect on both the capital stock and the gross investment. We can hypothesize about all of the characteristics two-way fixed effects handle, but note that it does not account for unit-specific changes over time.
Looking at the DAG, it is clear that time and unit-specific characteristics are confounders in the relationship between capital stock and gross investment. They act as open backdoors, as explained in Chapter 3 of Causal Inference: The Mixtape. Without controlling for them, a backdoor is left open. By using year and firm fixed effects, we close these backdoors. Let’s take a look.
Running Regressions
Generally speaking, there are better options than base R for fixed effects regressions, such as felm from the package lfe. For this first chunk, I will manually add fixed effects by adding factors within the base R lm command. While we would never report fixed effect coefficients in a table, I want to pull back the curtain on what these fixed effects actually do.
library(stargazer)
reg1 <- lm(inv~capital, data=Grunfeld)
reg2 <- lm(inv~capital + factor(firm), data=Grunfeld)
reg3 <- lm(inv~capital + factor(year), data=Grunfeld)
reg4 <- lm(inv~capital + factor(firm)+ factor(year), data=Grunfeld)
stargazer(reg1,reg2,reg3,reg4, type="text", df=FALSE)##
## ===============================================================
## Dependent variable:
## -------------------------------------------
## inv
## (1) (2) (3) (4)
## ---------------------------------------------------------------
## capital 0.477*** 0.371*** 0.538*** 0.414***
## (0.038) (0.019) (0.046) (0.026)
##
## factor(firm)2 -66.455*** -51.233**
## (21.236) (21.579)
##
## factor(firm)3 -413.682*** -402.993***
## (20.668) (20.564)
##
## factor(firm)4 -326.441*** -303.744***
## (22.546) (23.851)
##
## factor(firm)5 -486.278*** -479.318***
## (20.344) (19.973)
##
## factor(firm)6 -350.866*** -327.439***
## (22.697) (24.106)
##
## factor(firm)7 -436.783*** -422.426***
## (21.114) (21.362)
##
## factor(firm)8 -356.472*** -332.243***
## (22.866) (24.394)
##
## factor(firm)9 -436.170*** -421.079***
## (21.217) (21.546)
##
## factor(firm)10 -366.731*** -339.071***
## (23.641) (25.688)
##
## factor(year)1936 22.461 23.940
## (74.656) (27.617)
##
## factor(year)1937 27.899 32.948
## (74.677) (27.635)
##
## factor(year)1938 -36.689 -27.093
## (74.739) (27.688)
##
## factor(year)1939 -42.401 -30.798
## (74.779) (27.721)
##
## factor(year)1940 -11.429 0.583
## (74.788) (27.729)
##
## factor(year)1941 5.330 19.584
## (74.843) (27.775)
##
## factor(year)1942 -26.252 -8.639
## (74.942) (27.859)
##
## factor(year)1943 -36.399 -17.568
## (74.984) (27.893)
##
## factor(year)1944 -32.389 -13.759
## (74.977) (27.887)
##
## factor(year)1945 -33.057 -13.525
## (75.009) (27.914)
##
## factor(year)1946 -3.631 17.699
## (75.077) (27.972)
##
## factor(year)1947 -57.808 -27.241
## (75.520) (28.343)
##
## factor(year)1948 -73.111 -37.430
## (75.832) (28.602)
##
## factor(year)1949 -106.844 -66.762**
## (76.137) (28.854)
##
## factor(year)1950 -105.875 -63.286**
## (76.326) (29.011)
##
## factor(year)1951 -69.251 -23.910
## (76.547) (29.192)
##
## factor(year)1952 -76.610 -23.914
## (77.200) (29.725)
##
## factor(year)1953 -67.677 -5.127
## (78.217) (30.546)
##
## factor(year)1954 -112.634 -40.105
## (79.408) (31.492)
##
## Constant 14.236 367.613*** 39.207 354.917***
## (15.639) (18.967) (52.867) (26.085)
##
## ---------------------------------------------------------------
## Observations 200 200 200 200
## R2 0.439 0.918 0.467 0.931
## Adjusted R2 0.436 0.914 0.408 0.919
## Residual Std. Error 162.850 63.566 166.931 61.749
## F Statistic 154.937*** 212.745*** 7.845*** 78.785***
## ===============================================================
## Note: *p<0.1; **p<0.05; ***p<0.01It should be noted that you should never report a table with fixed effect coefficients, simply note at the bottom of the table for which columns fixed effects were used (shown in the next chunk). The coefficients are included here for the sake of this exercise. First, note how factor(firm)1 is not shown, nor is factor(year)1935. When a factor is added to a regression model, it creates a matrix of dummy variables, with one variable for each level of the factor. For example, all observations from 1940 have a 1 in the factor(year)1940 column and a 0 in all other year columns. All observations from firm 3 have a 1 in the factor(firm)3 column, and a 0 in all other firms columns. One level of the factor must be excluded as a “reference category”. The same way the coefficient on capital is essentially in relation to capital = 0, the year factor coefficients are all measured in relation to 1935 while the firm factors are all in relation to firm 1.
reg4 regresses investment on capital AND a dummy variable for each firm and each year (except for the reference categories). As seen in the plots earlier, firm 2 is simply a bit smaller than firm 1, and the other firms are substantially smaller (having levels of Y hundreds of points lower than firm 1.)
Let’s remake this table, but with felm, which is made for fixed effect regressions and automatically hides the coefficients. Additionally, it allows me to easily cluster my standard errors. Take a look back at the plot where we used an individual smoothing line for each firm. Do you notice how the fit varies from firm to firm? Firm 1 seems to have a much worse fit than some of the smaller firms. This gives us reason to believe that the error terms of our observations are correlated within the firms. If our model systemically predicts some firms better than others, it is best practice to cluster standard errors at the firm level. In felm, this is as trivial as |firm being added to the end of the formula. Clustered standard errors are usually larger than the classic analytic standard errors, leading to less over-rejection of the null hypothesis.
A few additions are made to the stargazer command here. I can recreate reg1 by using felm without fixed effects, or I can reuse it in stargazer and automatically have it labelled as OLS instead of felm in the table.
# note that the felm formula is felm(y~x|FE|IV|ClusterSE, data=data)
library(lfe)
fe2 <- felm(inv~capital|firm|0|firm, data=Grunfeld)
fe3 <- felm(inv~capital|year|0|firm, data=Grunfeld)
fe4 <- felm(inv~capital|firm+year|0|firm, data=Grunfeld)
stargazer(reg1,fe2,fe3,fe4, type="text", add.lines=list(c("Year FE?", "No","No","Yes","Yes"), c("Firm FE?", "No","Yes","No","Yes")), notes="SEs clustered at firm level.", df=FALSE, dep.var.labels="Gross Investment", covariate.labels = "Capital Stock")##
## =========================================================
## Dependent variable:
## -------------------------------------
## Gross Investment
## OLS felm
## (1) (2) (3) (4)
## ---------------------------------------------------------
## Capital Stock 0.477*** 0.371*** 0.538*** 0.414***
## (0.038) (0.065) (0.170) (0.060)
##
## Constant 14.236
## (15.639)
##
## ---------------------------------------------------------
## Year FE? No No Yes Yes
## Firm FE? No Yes No Yes
## Observations 200 200 200 200
## R2 0.439 0.918 0.467 0.931
## Adjusted R2 0.436 0.914 0.408 0.919
## Residual Std. Error 162.850 63.566 166.931 61.749
## F Statistic 154.937***
## =========================================================
## Note: *p<0.1; **p<0.05; ***p<0.01
## SEs clustered at firm level.Note that intercepts are not displayed for the fixed effects regressions. This is because the intercept term is unique for each factor of the fixed effects. In other words, an intercept adjustment is made for each firm and/or year. The fixed effects coefficients in the verbose table from before are the unit and year-specific intercepts!3 Based on the limited information we have, we would assume that the estimate of 0.414 is likely the best estimate we have for how capital stock “affects” investment. For each dollar increase in capital stock, we expect investment to be about 41 cents higher.
Keep in mind that many intercepts are not literally interpretable in this way; capital stock is never 0 in this dataset. The intercept simply provides an adjustment for the starting level of y.↩︎
Even if some firms are affected differentially by the war (e.g. more employees who enlist), any part of the effect that is not firm-specific can be captured by year fixed effects.↩︎
The constant displayed in the overly verbose table is, interestingly enough, the “coefficient” for the reference category.↩︎